General Rhomb Tiling Model.
( Section II of rhomb tiling paper )
We will denote a rhomb prototile with opening angle ![]() as
as ![]() and the corresponding substitution rhomb tile as
and the corresponding substitution rhomb tile as ![]() . The model is based on the observation that the combined area of the pair of rhomb prototiles
. The model is based on the observation that the combined area of the pair of rhomb prototiles ![]() and
and ![]() is proportional to the area of the rhomb prototile
is proportional to the area of the rhomb prototile ![]() , the proportionality factor
, the proportionality factor ![]() being independent of
being independent of ![]() . Consequently, substitution tiles
. Consequently, substitution tiles ![]() may be constructed from a combination of prototiles
may be constructed from a combination of prototiles ![]() and pairs of tiles
and pairs of tiles ![]() . If
. If ![]() and
and ![]() are their numbers respectively, the ratio of the area of
are their numbers respectively, the ratio of the area of ![]() and
and ![]() is
is
(1) ![]()
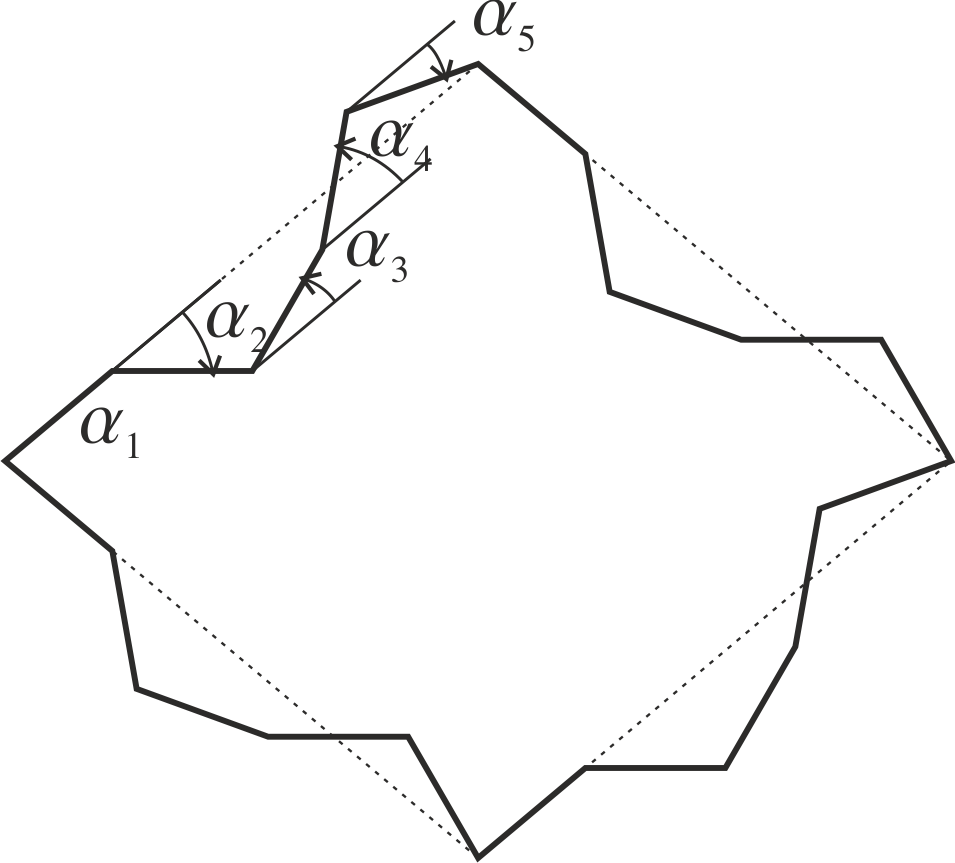
 occur in
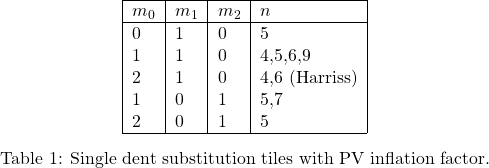
occur in 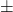 pairs or are zero. In this example we chose the edge angles
pairs or are zero. In this example we chose the edge angles 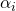 to be
to be 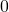 ,
, 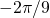 ,
, 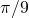 ,
, 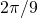 ,
, 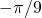 respectively. All edges have congruent shapes. The lower and upper left edges are related by a rotation over the opening angle
respectively. All edges have congruent shapes. The lower and upper left edges are related by a rotation over the opening angle 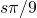 with respect to the left corner. Similarly, the lower and upper right edges are related by a rotation over the opening angle with respect to the right corner. Opposite edges are related by a translation.
with respect to the left corner. Similarly, the lower and upper right edges are related by a rotation over the opening angle with respect to the right corner. Opposite edges are related by a translation.A second requirement for a tiling of the entire plane is to realize proper edge substitutions. We will assume that all four substitution tile edges have the same shape. Neighbouring edges at the opening angle are related by a rotation over that angle and opposite edges are related by a translation (Fig. M1). This edge arrangement also ensures that the substitution tile area is equal to the inflated rhomb area, and, therefore, ![]() is equal to the areal scaling factor. The angles between the outer prototile edges and the substitution tile rhomb edge will be called the edge angles
is equal to the areal scaling factor. The angles between the outer prototile edges and the substitution tile rhomb edge will be called the edge angles ![]() . For now, we will assume that overhangs are not allowed and
. For now, we will assume that overhangs are not allowed and ![]() . The length of the substitution tile rhomb edge
. The length of the substitution tile rhomb edge
(2) ![]()
is the inflation factor of the rhomb tiles. Because the areal scaling factor ![]() is the square of
is the square of ![]() , equations 1 and 2 can be combined into
, equations 1 and 2 can be combined into
(3) ![]()
This equality can only be satisfied if the arguments ![]() and
and ![]() are both equal to an integer times
are both equal to an integer times ![]() for all
for all ![]() and
and ![]() . There are two solutions: either all angles
. There are two solutions: either all angles ![]() are equal to an integer times
are equal to an integer times ![]() , or all of them are equal to a half-integer times
, or all of them are equal to a half-integer times ![]() .
.
Because the beginning and end of the substitution edge have to be at the endpoints of the substitution tile rhomb edge, the following relationship between the edge angles ![]() should be met:
should be met:
(4) ![]()
A general solution of is that the edge angles ![]() occur in
occur in ![]() -pairs or are zero.
-pairs or are zero.
There are also special solutions. For instance, if one requires that the sum of three terms is zero, one finds that ![]() and
and ![]() . This solution is valid if
. This solution is valid if ![]() is a multiple of 3. An example satisfying this condition is the Lord tiling, having edge angles
is a multiple of 3. An example satisfying this condition is the Lord tiling, having edge angles ![]() and
and ![]() \cite{HarrissFrett}.
\cite{HarrissFrett}. ![]() in this case, and the edge sequence is
in this case, and the edge sequence is ![]() . In this paper, however, we will only consider the more general
. In this paper, however, we will only consider the more general ![]() pairing condition.
pairing condition.
In the general case equation 3 becomes
(5) ![]()
or
(6) ![]()
Equations 5 or 6 determine the type and number of prototiles ![]() from which the substitution tile can be constructed, once the shape of the substitution tile edge has been chosen. In view of the above considerations, this edge shape may be characterized by a sequence of integers or half-integers, the \textit{edge sequence}
from which the substitution tile can be constructed, once the shape of the substitution tile edge has been chosen. In view of the above considerations, this edge shape may be characterized by a sequence of integers or half-integers, the \textit{edge sequence} ![]() , defined by
, defined by ![]() ,
, ![]() \cite{Maloney14}.
\cite{Maloney14}.
If the finite edge angles are present as pairs in accordance with equation 4, always a valid solution for the substitution tile is obtained, because both sides may be written as a sum of cosine terms having even valued coefficients. The pairing of the edge angles, therefore, guarantees that the substitution tiles are composed of an integer number of prototiles.
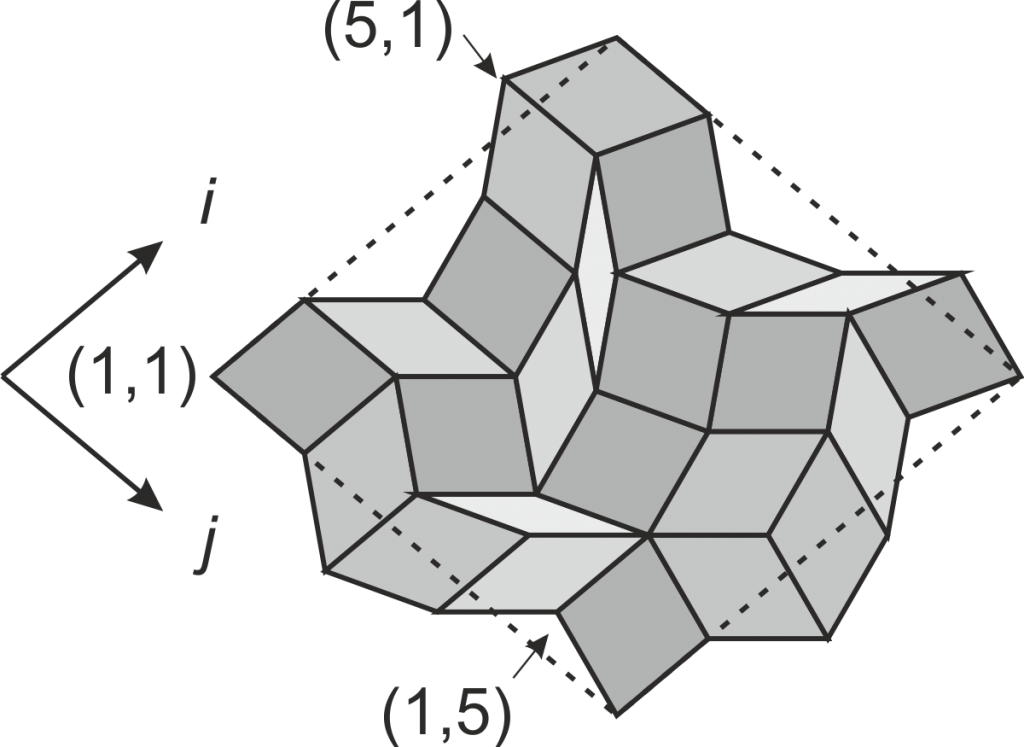
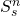 with a given edge shape. The prototile at position
with a given edge shape. The prototile at position 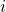 ,
,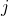 is
is 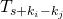 , where 4
, where 4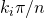 and
and 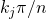 are the edge angles at the upper and lower left edges respectively.
are the edge angles at the upper and lower left edges respectively.Equations 5 or 6 constitute a connection between the prototile edge angle pairs ![]() and the numbers of prototiles in a substitution tile
and the numbers of prototiles in a substitution tile ![]() , not their arrangement. The relations do not guarantee that a consistent set of substitution tiles can be found. However, in the following we will show that a general set of substitution rhomb tiles can be constructed for arbitrary
, not their arrangement. The relations do not guarantee that a consistent set of substitution tiles can be found. However, in the following we will show that a general set of substitution rhomb tiles can be constructed for arbitrary ![]() and for an arbitrary substitution tile edge shape.
and for an arbitrary substitution tile edge shape.
We start with a construction of the circumference of the tile ![]() as described earlier and illustrated in Fig.~??. Next, copies of the edges are translated to the breaks of neighbouring edges. If the breaks of the upper and lower left edge are indexed as
as described earlier and illustrated in Fig.~??. Next, copies of the edges are translated to the breaks of neighbouring edges. If the breaks of the upper and lower left edge are indexed as ![]() and
and ![]() respectively, starting at the left corner as indicated in Fig.~??), one obtains a grid of vertices
respectively, starting at the left corner as indicated in Fig.~??), one obtains a grid of vertices ![]() , at which four prototiles meet. The one bounded by the vertices
, at which four prototiles meet. The one bounded by the vertices ![]() ,
, ![]() ,
, ![]() and
and ![]() is a prototile of the type
is a prototile of the type ![]() . The vertices at diagonal positions are occupied by tiles
. The vertices at diagonal positions are occupied by tiles ![]() , whereas one can find pairs of tiles
, whereas one can find pairs of tiles ![]() at off-diagonal positions
at off-diagonal positions ![]() and
and ![]() . This general substitution rule may be represented by the following matrix
. This general substitution rule may be represented by the following matrix
(7) 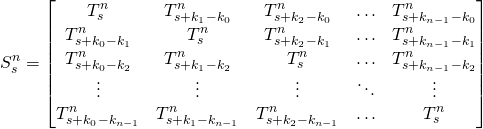
For later use one should note, that the prototiles parallel to the substitution edges, i.e. the rows or columns of the matrix, form worms, and the edges of the worms have shapes identical to the edge shape of the substitution tile.
The prototiles are allowed to have indices ![]() or
or ![]() . These prototiles will have negative areas, meaning that they have to be subtracted from the tiling. We consider a tiling of the plane to be a legitimate one, if in the end there are no holes or overlaps. So, negative or subtraction tiles are allowed, if they remove all overlaps between tiles and do not leave holes in the tiling. In one of the next sections, we will reason, that this is presumably the case for substitution edges without loops. Also the zero area prototiles for which
. These prototiles will have negative areas, meaning that they have to be subtracted from the tiling. We consider a tiling of the plane to be a legitimate one, if in the end there are no holes or overlaps. So, negative or subtraction tiles are allowed, if they remove all overlaps between tiles and do not leave holes in the tiling. In one of the next sections, we will reason, that this is presumably the case for substitution edges without loops. Also the zero area prototiles for which ![]() or
or ![]() play a important role in our scheme and cannot simply be neglected.
play a important role in our scheme and cannot simply be neglected.
Substitution Matrices.
Here we want to reformulate the rhomb substitution model in terms of the edge and tile substitution matrices.
If overhangs are included, the prototile edges in a tiling will point into ![]() directions. Each of these is replaced by a number of prototile edges in orientations determined by the edge sequence, i.e.
directions. Each of these is replaced by a number of prototile edges in orientations determined by the edge sequence, i.e. ![]() in the same,
in the same, ![]() in the opposite direction and
in the opposite direction and ![]() with
with ![]() in directions differing by
in directions differing by ![]() and
and ![]() . The edge substitution matrix, therefore, is
. The edge substitution matrix, therefore, is
(8) 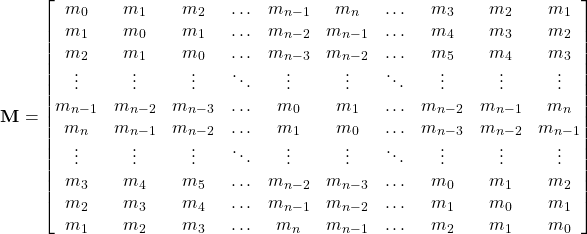
A tile with index ![]() is substituted by
is substituted by ![]() prototiles with index
prototiles with index ![]() ,
, ![]() with index
with index ![]() and
and ![]() with index
with index ![]() and
and ![]() , with
, with ![]() and
and ![]() . So the substitution matrix
. So the substitution matrix ![]() is
is
(9) 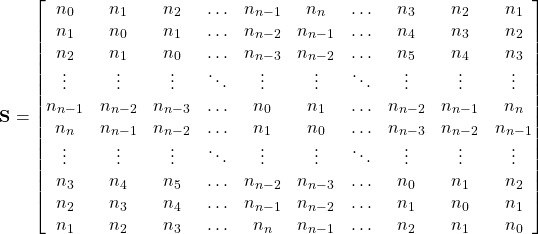
The relation between the tile and edge substitution matrices is
(10) ![]()
This matrix equation may be used to calculate the numbers of prototiles in a substitution tile for a given edge shape instead of equations 5 .
The ![]() are given by the product of the first row and the
are given by the product of the first row and the ![]() -th column
-th column
(11) ![]()
Both ![]() and
and ![]() are
are ![]()
![]() matrices \cite{Kra12}.
matrices \cite{Kra12}.
Consequently, a shorthand notation of equations 8 and 9 is
(12) ![]()
(13) ![]()
All ![]() matrices are known to have the same set of normalized eigenvectors
matrices are known to have the same set of normalized eigenvectors
(14) ![]()
with ![]() and
and ![]() .
.
The eigenvalues of ![]() are
are
(15) ![]()
, and because of relation ![]() , those of
, those of ![]() are
are ![]() .
.
The eigenvector ![]() is equal to the inflation factor
is equal to the inflation factor
(16) ![]()
A substitution tiling can only be a model set for a quasi crystal if its inflation factor is a Pisot- or PV-number \cite{Meyer95}, because a model set is point diffractive \cite{Hof95}. ![]() is a PV-number, if the absolute value of all its conjugates is less than 1. The conjugate eigenvalues are the ones for
is a PV-number, if the absolute value of all its conjugates is less than 1. The conjugate eigenvalues are the ones for ![]() coprime to
coprime to ![]() . Using the above formulae we find that the inflation factors are PV-numbers in the following
. Using the above formulae we find that the inflation factors are PV-numbers in the following ![]() or
or ![]() or socalled
or socalled ![]() cases:
cases:
The edge substitution matrix for a halfinteger edge sequence can be obtained by doubling the ![]() value. The fractional indices have to be doubled as well and become the
value. The fractional indices have to be doubled as well and become the ![]() values for odd k, whereas the
values for odd k, whereas the ![]() for even k are zero. From table ?? it is clear that the half integer single dent substitution tiles will not have PV inflation factors.
for even k are zero. From table ?? it is clear that the half integer single dent substitution tiles will not have PV inflation factors.