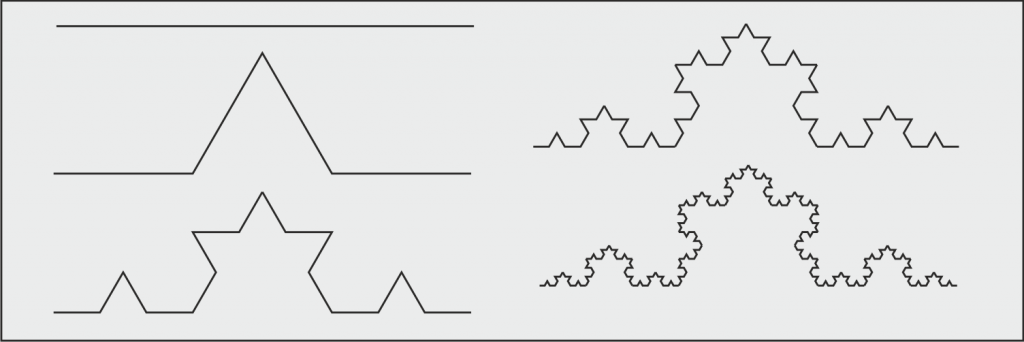
The mathematician Niels Fabian Helge von Koch (1870-1924) invented a famous curve by iteratively breaking up a line segment into three line segments of equal length and by replacing the central one by an equilateral triangle and removing the base line of the triangle. This produces a fractal geometry (Fig. K1)
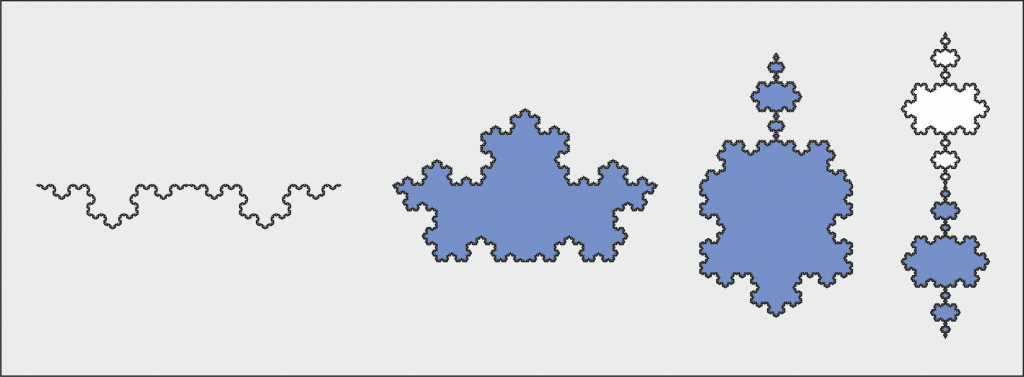
The edges of our type b) ![]() rhomb tilings are reminiscent of these Koch curves as shown in Fig. K2. The main difference is that our building instruction is different. At each new iteration n, all the line segments are replaced by a dent or a dimple with a connecting angle of 120 degrees. The edges for even n are identical to the Koch curves.
rhomb tilings are reminiscent of these Koch curves as shown in Fig. K2. The main difference is that our building instruction is different. At each new iteration n, all the line segments are replaced by a dent or a dimple with a connecting angle of 120 degrees. The edges for even n are identical to the Koch curves.

By applying substitution rule b) repeatedly, the circumference of our rhomb tiles also gets a fractal appearance (Fig. K3).
 ,
,  rule b)
rule b)Koch curves can be connected to form so called Koch Snowflakes or Koch Islands. Below four snowflake tiles are shown using the same edge. To the left the curve is decorating the edge of a triangle either at the outside or at the inside. To the right the curve is decorating a hexagon. Note, that the inside decorated hexagon is identical to a next generation outside decorated triangle.
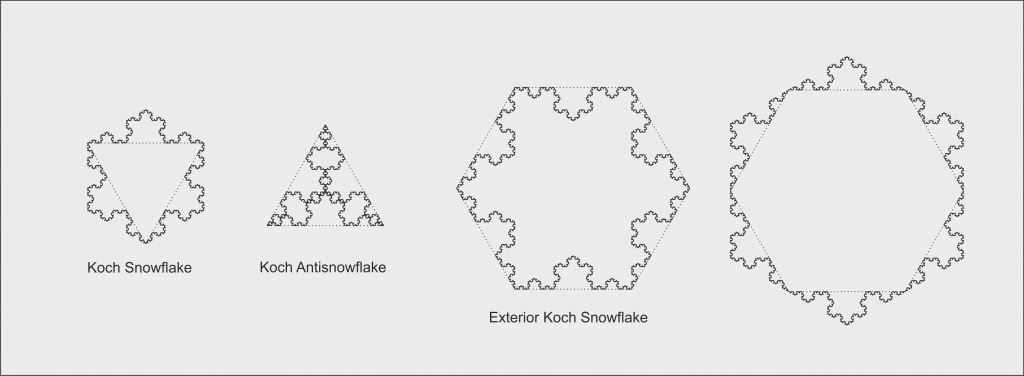
Periodic tilings of the plane may be achieved by using two or more Koch tiles. Examples can be found on the Koch Snowflake Wikipedia page. Below, two special tilings with differently sized Koch tiles are shown, one with small and one with a large snowflake in the center. The first one is related to the circle limits of M.C.Escher (van Dusen et. al.).
Fig. K5. Hexagonal Koch Tilings
Fig. K6. Pentagonal Koch Tilings.



